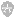材料力学中截面的几何属性
本文主要对材料力学中的几个截面几何属性进行简单介绍,包括惯性矩、极惯性矩、静矩、惯性积和惯性半径。一、概述对于长度方向尺寸远大于截
本文主要对材料力学中的几个截面几何属性进行简单介绍,包括惯性矩、极惯性矩、静矩、惯性积和惯性半径。


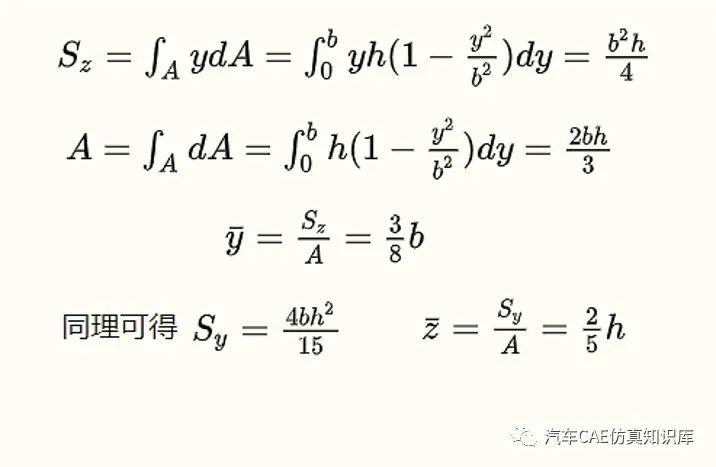
一、概述
对于长度方向尺寸远大于截面尺寸的杆件,其截面的形状在很大程度上就决定了结构的力学性能。而截面的几何属性完全由截面形状决定,并可直接反映杆件在不同受力状态下的性能参数。
对于常见的截面几何属性,主要的应用可概括如下:
1、惯性矩:计算纯弯曲变形杆截面的正应力;
2、极惯性矩:计算扭转变形杆截面切应力,与扭转刚度相关;
3、静矩:计算截面形心;
4、惯性积:惯性积等于零时对应的坐标系为主坐标系,此时惯性矩取最大和最小值;
5、惯性半径:计算压杆稳定性。
二、惯性矩
1、定义:Moment of inertia of an area,截面上所有点至坐标轴距离平方的和。
2、关键点释义:惯性矩是一个几何量,可反映截面上的点相对于轴的分布情况。通常被用作描述截面抵抗弯曲的性质,国际单位为(m4),即面积二次矩,因此也称其为面积惯性矩。需要注意的是,它与质量惯性矩(即转动惯量)是不同的概念。
惯性矩可用于计算纯弯曲变形杆截面上的正应力σ=M*y/Iz,其中M为截面所受弯矩,y为点与坐标轴Z的距离,Iz为截面对Z轴的惯性矩。截面上的点离Z轴越远,截面对Z轴的惯性矩越大,则截面抵抗弯曲变形的能力越强。
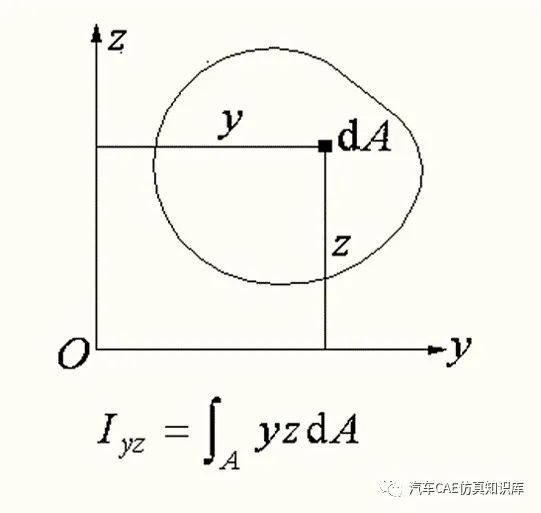
3、计算方法,示例说明如图1所示。

图1 计算示例
可知,面积元素dA对于z轴或y轴的惯性矩为dA与其至z轴或y轴距离平方的乘积、然后再积分。惯性矩值恒大于0,其大小与坐标系位置有关。
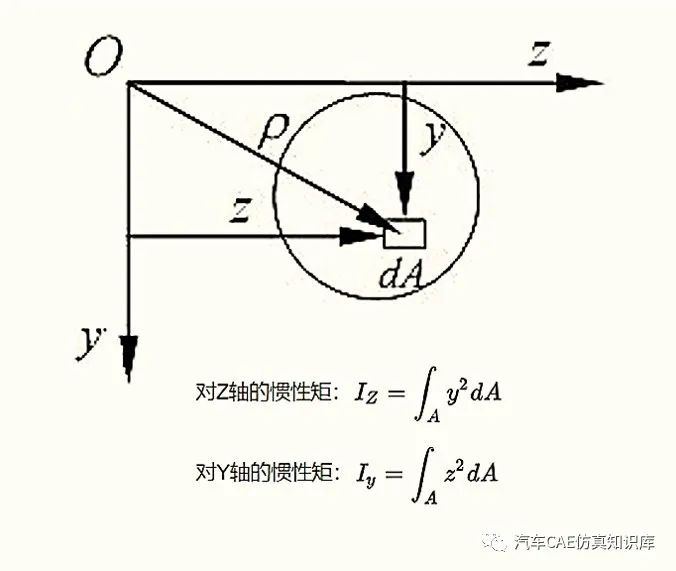
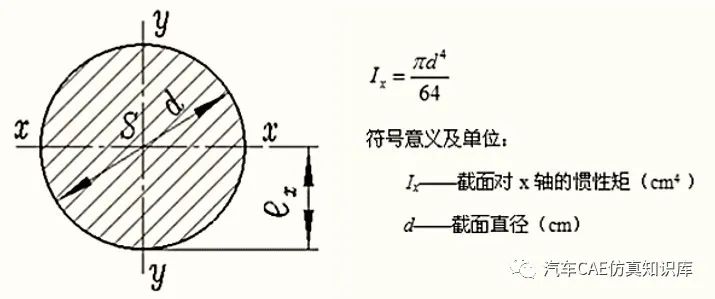
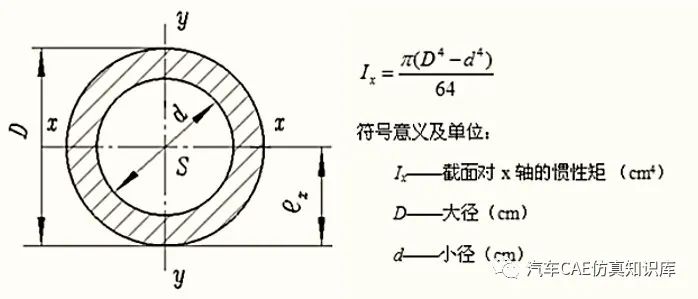
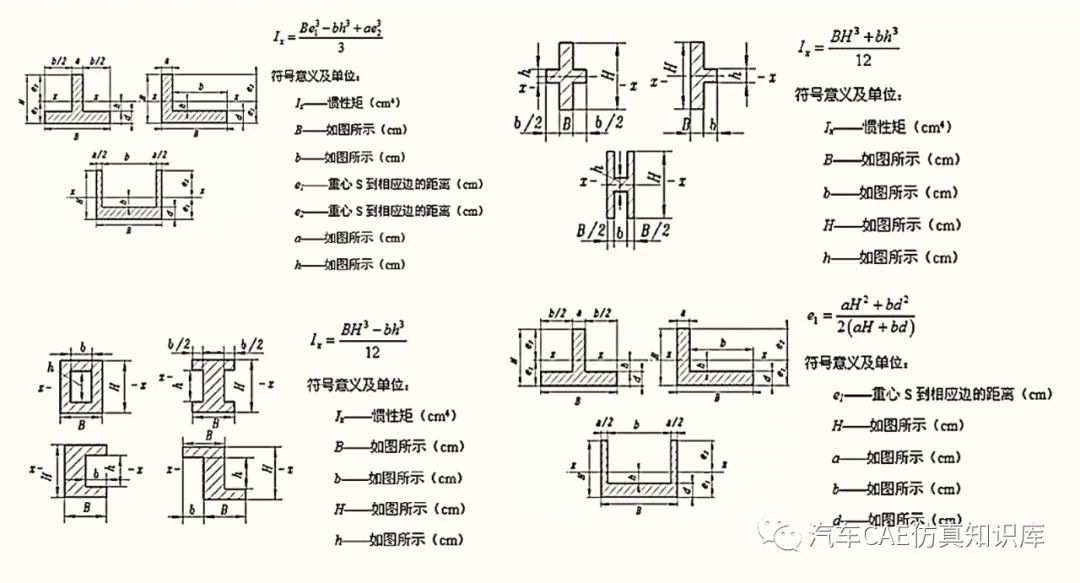
常见的圆柱截面、圆环截面和矩形截面的惯性矩计算如图2~图4所示,其他截面的惯性矩计算如图5所示。

图2 圆形截面的惯性矩

图3 圆环截面的惯性矩

图4 矩形截面的惯性矩

图5 其他截面的惯性矩
需要说明的是,坐标系不同时计算公式也不相同。
三、极惯性矩
1、定义:Polar moment of inertia,指面上所有点到某点的距离平方的和。
2、关键点释义:极惯性矩可反映截面上的点相对于某点的分布情况,与横截面和尺寸有关,是计算抗扭截面系数的一个重要物理量。极惯性矩始终大于0,其大小与坐标系位置有关,国际单位为(m4)。
极惯性矩可用于计算杆件在扭转状态下的最大切应力τ=M*ρ/Ip,其中M为截面承受的扭矩,ρ为点与圆心间的距离,Ip为截面对圆心的极惯性矩。截面上离轴心较远的点越多,截面对轴心的极惯性矩越大,则截面抵抗扭转变形的能力越强。
3、计算方法:其计算公式可表达为Ip=∫Aρ2dA。参考图1可知,ρ2=y2+z2,所以截面对坐标原点的极惯性矩等于截面对两个坐标轴的惯性矩之和,且无论坐标系如何移动和旋转,上述关系始终满足。
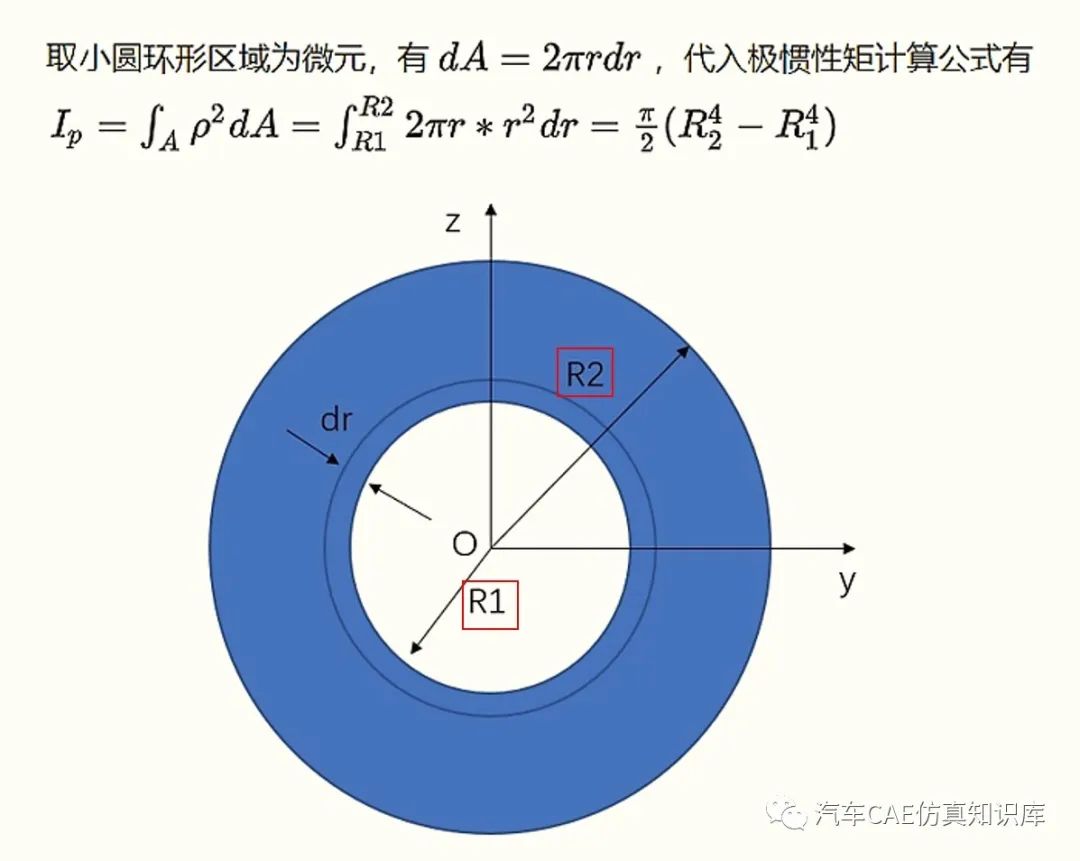
以圆环为例,极惯性矩的推导计算如图6所示。

图6 极惯性矩的计算推导
可知,当R1为0时,即为圆形截面的极惯性矩。由于Ip是衡量截面抗扭性能的参数,因此对于圆形截面和圆环截面,可直接由Ip来计算抗扭截面系数Wt=Ip/R,(R是外圆半径);然后由Wt可得扭转时的最大切应力τmax=T/Wt,(T为扭矩);Ip还可用来计算扭转角φ=Tl/GIp,(l为轴长,G为材料的剪切模量,其值等于E/(2(1+u)),E为弹性模量,u为泊松比;由于是“极”,所以扭转角的单位是rad),其倒数即为扭转刚度。
对于非圆截面,如图4的矩形截面,相关公式如图7所示。

图7 矩形截面相关计算
四、静矩
1、定义:Static moment,平面图形的面积A与其形心到某一坐标轴的距离的乘积称为平面图形对该轴的静矩。
2、关键点释义:静矩一般用S来表示,其值可能为正,可能为负,也可能为0;量纲为长度的3次方,又称为截面面积矩。
静矩可用于计算截面形心。截面对某轴的静矩为零,则该轴必过形心,截面对一个坐标系的两个轴的静矩都为零,则该坐标系原点为形心。
3、计算方法:截面对Z轴的静矩为Sz=∫AydA,截面对Y轴的静矩为Sy=∫AzdA。形心的坐标为静矩与面积A的比值。
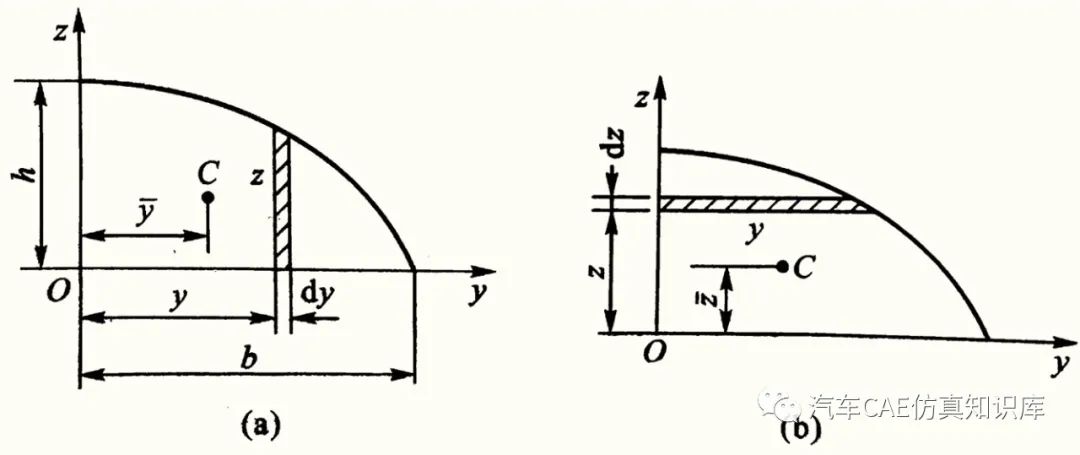
如图8所示,以抛物线(方程为z=h(1-y2/b2))为例,计算由抛物线、y轴和z轴所围成的平面图形对y轴和z轴的静矩,并确定图形的形心。

图8 抛物线示意图
取微元dA=zdy=h(1-y2/b2)dy,代入静矩计算公式可得截面对Z轴的静矩Sz,同时可推导图形的面积A,这样二者相除就可得到y方向的形心坐标。同理可得到z方向的形心坐标。计算过程公式如图9所示。
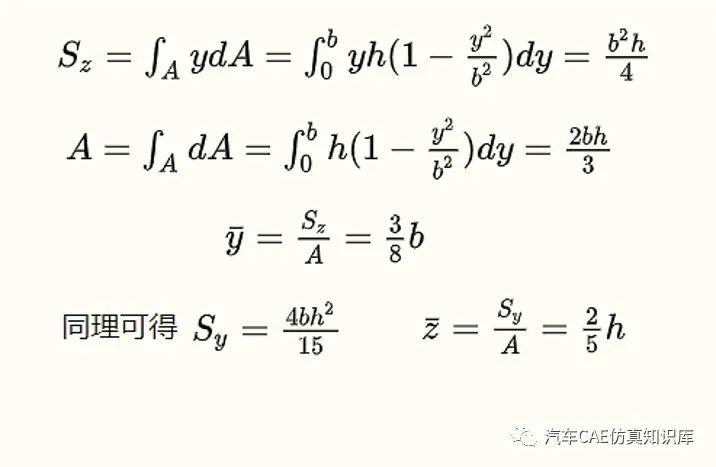
图9 静矩和图形面积
五、惯性积(面积)
1、定义:Product of inertia,指截面上所有点横纵坐标之积的和。
2、关键点释义:惯性积大小可能为正,也可能为负,其大小与坐标系有关,量纲为长度的四次方。
惯性积可用于确定主惯性轴。过某点取坐标系,当截面对该坐标系的惯性积等于零时,这一对坐标系称为主惯性轴,简称主轴。通过截面形心的主惯性轴称为形心主惯性轴,截面对该轴的惯性矩称为形心主惯性矩。由平行移轴公式可知,截面对过形心主惯性轴的惯性矩是截面对所有坐标系惯性矩中最大和最小的两个惯性矩。
3、计算方法:如图10所示。

图10 惯性积的计算
六、惯性半径
1、定义:Radius of gyration,又称回转半径,是指物体微分质量假设的集中点到转动轴间的距离。
2、关键点释义:惯性半径可用于使用欧拉公式计算杆受压发生屈曲时的临界应力。
3、计算方法:惯性半径值为任一截面对某轴的惯性矩除以该截面面积所得商的平方根值,它的大小也等于转动惯量除总质量后再开平方。
即Iz=∫Ay2dA=A*iz2,或iz=(Iz/A)1/2,iz即为截面对z轴的惯性半径。
最后需要说明的是,由于惯性矩、极惯性矩、惯性积的计算公式中的被积函数都是二次项,因此统称为二阶矩;静矩计算公式中的被积分项是一次项,因此称为一阶矩。
相关热词搜索:材料力学 惯性矩 极惯性矩 静矩 惯性积 惯性半径
上一篇:碳纤维复合材料的知识盘点
下一篇:什么是复合材料?全球知名科研材料供应商
版权与免责声明:本网转载并注明自其它来源(非本站原创)的作品,目的在于传递更多信息,并不代表本网赞同其观点或和对其真实性负责,不承担此类作品侵权行为的直接责任及连带责任。其他媒体、网站或个人从本网转载时,必须保留本网注明的作品第一来源,并自负版权等法律责任。
如涉及作品内容、版权等问题,请在作品发表之日起一周内与本网联系,否则视为放弃相关权利。
分享到:
 收藏
收藏
 收藏
收藏
热门评论
今日焦点
热门话题
- 52航空发动机涡轮叶片的服役环境及材料...
- 47十大航空焊接技术,你了解哪几种?
- 27树脂基复合材料连续超声波焊接技术
- 15材料力学中截面的几何属性
- 13碳纤维增强复合材料(CFRP)在军工领...
- 12航空航天系统结构材料研究进展综述 ⑾
- 10高性能复合材料的十大常见应用领域
- 10什么是复合材料?全球知名科研材料供应商
- 10虚拟样机 | 使用虚拟样机技术优化...
- 9材料小知识--复合材料
- 9八大金属材料成形工艺,你都知道吗?
- 6民用航空产品的可用性
- 6复合材料胶接修复飞机金属结构关键技...
- 6钛合金在航空航天应用中的焊接技术
- 5宾大团队设计新型智能复合材料体系,...
- 5民机复材液氢罐的研发要点
- 5动态感应焊接技术—用于航空大尺寸热...
- 4树脂基复合材料连续感应焊接技术及航...
- 4碳纤维复合材料的知识盘点
- 3分层缺陷深度对复合材料层合板力学性...